Регистры, срабатывающие по фронту
Принцип действия регистров, срабатывающих по фронту тактового сигнала, ничем не отличается от принципа действия D-триггера. По положительному фронту тактового сигнала С каждый из выходов регистра устанавливается в тот уровень, который был в этот момент на соответствующем данному выходу входе D, и сохраняется таковым до прихода следующего положительного фронта сигнала С. То есть если триггер запоминает один сигнал (один двоичный разряд, один бит), то регистр запоминает сразу несколько (4, 6, 8, 16) сигналов (несколько разрядов, битов). Память регистра сохраняется до момента выключения питания схемы.
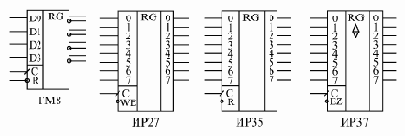
Рис. 8.2. Параллельные регистры стандартных серий, срабатывающие по фронту
В стандартные серии входит несколько типов параллельных регистров, срабатывающих по фронту (рис. 8.2). Различаются они количеством разрядов, наличием или отсутствием инверсных выходов, наличием или отсутствием входа сброса (–R) или разрешения записи (–WE), а также типом выходных каскадов (2С или 3С) и, соответственно, наличием или отсутствием входа разрешения –EZ. Иногда на схемах тактовый вход С обозначается WR - сигнал записи в регистр.
Большинство регистров имеют восемь разрядов, то есть запоминают один байт информации. Регистр ТМ8 в справочниках обычно называется счетверенным D-триггером (он и в наименовании несет буквы ТМ), хотя он вполне может рассматриваться и как регистр, так как тактовый вход С и вход сброса –R у всех четырех триггеров объединены между собой.
Таблицы истинности регистров очень просты и не отличаются принципиально от таблицы истинности D-триггеров. Отличие от триггеров появляется только в случае наличия у регистра дополнительных управляющих входов разрешения записи –WE и разрешения выхода –EZ. В качестве примеров в табл. 8.1 приведена таблица истинности регистра ИР27, а в табл. 8.2 - регистра ИР37. По переходу тактового сигнала С из 0 в 1 (положительный фронт) оба регистра записывают в себя входную информацию.
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 0 | X | Не меняется | |
| 0 | 1 | Х | Не меняется | |
| 1 | Х | Х | Не меняется | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 0 | X | Не меняется | |
| 0 | 1 | Х | Не меняется | |
| 1 | Х | Х | Z | |
p>Все регистры, имеющие выход с тремя состояниями, обеспечивают повышенную нагрузочную способность. Задержка переключения регистров примерно соответствует задержке переключения триггеров. Все временные ограничения, накладываемые на входные сигналы в случае триггеров, справедливы и для входных сигналов регистров. Например, не должна быть слишком малой длительность сигнала С, а также не должна быть слишком малой задержка между установлением сигнала D и приходом положительного фронта сигнала С. Иначе работа регистра может быть нестабильной или даже неправильной.
Одно из основных применений регистров состоит в хранении требуемого кода в течение нужного времени. Если для работы остальной части схемы необходимо иметь входной код, который можно легко изменять, то для этого как раз подходит регистр.

|
Курсы | Учебные программы | Учебники | Новости | Форум | Помощь
Телефон: +7 (495) 253-9312, 253-9313, факс: +7 (495) 253-9310, email: info@intuit.ru © 2003-2007, INTUIT.ru::Интернет- Университет Информационных Технологий - дистанционное образование |
Рис. 8.5. Работа последовательной цепочки двух узлов
Иначе код на выходе цепочки может никогда не принять устойчивого значения, так как переходный процесс предыдущего такта будет сменяться переходным процессом следующего такта. То есть быстродействие узлов накладывает жесткое ограничение на тактовую частоту.
Однако можно обойти это ограничение, если воспользоваться принципом конвейера, заставить узлы работать не последовательно, а параллельно. Это достигается включением между узлами регистра, тактируемого входным тактовым сигналом. Еще один регистр целесообразно включить на входе второго узла, что обеспечит длительность устойчивого кода на выходе всего устройства, равную длительности периода тактового сигнала Т (рис. 8.6). В результате ограничение на период тактового сигнала становится более мягким: Т не должно быть меньше максимальной из двух величин t1 и t2 с добавлением времени задержки регистра:
T>max{t1,t2}+tRG
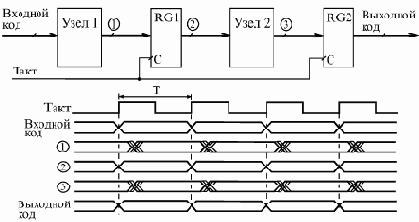
Рис. 8.6. Конвейерная обработка с помощью регистров
То есть к следующему фронту тактового сигнала должен закончить свою работу самый медленный из узлов, и тогда его выходной код будет записан в регистр правильно.
Точно так же можно построить конвейер на любое количество последовательно включенных узлов. Конечно, в результате введения конвейера происходит задержка выполнения полной функции устройства на число тактов, равное числу введенных регистров. Однако в том случае, когда необходимо обрабатывать большие последовательности входных кодов, эта задержка наблюдается только один раз - в самом начале последовательности, а затем уже она не имеет значения.
Регистры могут также применяться в составе вычислителей, выполняя функцию накопителя результата вычисления. В данном случае мы уже имеем дело с более сложной обработкой информации, чем при чисто комбинационных схемах. С каждым тактом в регистре обновляется содержимое, являющееся результатом математической обработки входного кода и результата предыдущего вычисления.
Рассмотрим два примера схем таких вычислителей.
Первая схема известна как накапливающий сумматор, применяющийся, например, в цифровых генераторах аналоговых сигналов.
В самом названии схемы отражена ее функция: она суммирует и накапливает результат. Накапливающий сумматор (рис. 8.7) состоит из сумматора и выходного регистра, охваченных обратной связью.
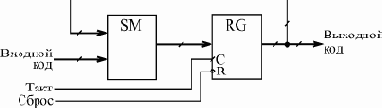
Рис. 8.7. Структура накапливающего сумматора
То есть на один вход сумматора подается код с выходов регистра, а на другой вход - входной код. В результате с каждым следующим фронтом тактового сигнала в регистр записывается код суммы входного кода с предыдущим содержимым регистра, с предыдущей суммой. Например, если входной код равен 3, а в регистре записан код 6, то в следующем такте в регистр будет записан код 9 (то есть 6 + 3), в следующем такте - код 12 (то есть 9 + 3) и т.д. Получается, что на выходе накапливающего сумматора формируется равномерно увеличивающийся двоичный код, и шаг этого увеличения можно менять. В данном случае удобно применять регистр со сбросом, например, ИР35.
Отметим три особенности накапливающего сумматора.
Во-первых, когда выходной код достигает максимальной величины (становится больше 2n, где n - количество разрядов регистра), происходит переполнение схемы и возобновление ее работы с минимальных значений кода. Однако совсем не обязательно в следующем цикле работы будут повторены те же значения кода, что и в предыдущем. Например, пусть n равняется 4, то есть максимальное число на выходе регистра равно 1111 в двоичном коде или 15 в десятичном коде. Пусть входной код равен 3. Тогда после начального сброса регистра выходной код будет нарастать так: 0, 3, 6, 9, 12, 15, 2, 5, 8, 11, 14, 1, 4, .… Это происходит потому, что суммирование чисел 15 и 3 даст 18 или, в двоичном коде, 10010, а так как мы работаем только с младшими четырьмя разрядами, у нас получится 0010 или 2.
Во-вторых, особенность накапливающего сумматора состоит в том, что при больших значениях входного кода (больших половины максимально возможной величины) он может рассматриваться как накапливающий вычитатель. Пусть, например, входной код 4-разрядного сумматора равен 15 (1111 в двоичном коде), а в регистре записано число 13 (1011 в двоичном коде).
В следующем такте в регистр запишется сумма 1101 + 1111 = 11100, а без старшего разряда - 1100, то есть 12. То есть выходной код уменьшился на единицу.
Наконец, в-третьих, совсем не обязательно шаг нарастания выходного кода накапливающего сумматора должен быть целым числом (то есть 0, 1, 2, 3, ...). Если в качестве выходного кода берутся не все, а только старшие разряды регистра, то шаг нарастания вполне может быть дробным, например, 0,5, 1,25 или 3,75. Не вошедшие в выходной код разряды будут иметь вес 2-1 (то есть 0,5), 2-2 (то есть 0,25) и т.д. Правда результат суммирования в выходном коде будет представлен с точностью до целых чисел. При этом возможна ситуация, когда в течение нескольких тактов код на выходе не меняется, например, при входном коде 0,5 выходной код будет меняться один раз на два такта, а при входном коде 0,25 - один раз на четыре такта.
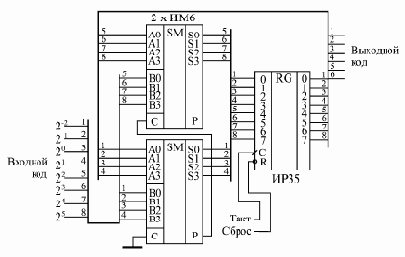
Рис. 8.8. Накапливающий сумматор
На рис. 8.8 показана схема 8-разрядного накапливающего сумматора на двух микросхемах сумматоров ИМ6 и одном регистре ИР35. В качестве выходного кода используется только 6 старших разрядов с выхода регистра, поэтому задание шага приращения возможно с точностью до 0,25. Максимально возможная частота тактового сигнала может быть определена по формуле T > tSM + tRG, где Т - период тактового сигнала, tSM - задержка 8-разрядного сумматора, а tRG - задержка регистра.
Последний пример применения регистров, который мы рассмотрим, - это вычислитель максимального значения входного кода. Такой вычислитель, например, может применяться в схемах цифровых осциллографов для измерения амплитуды входного аналогового сигнала.
Пусть мы имеем последовательность входных кодов, и нам необходимо выявить экстремальный (то есть максимальный или минимальный) код из всей этой последовательности. Эта задача решается довольно просто путем применения компаратора кодов и регистра, охваченных обратной связью (рис. 8.9).
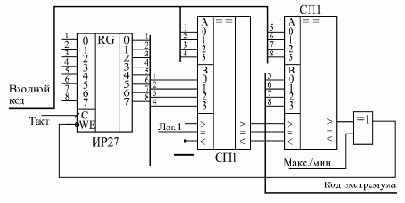
Рис. 8.9. Вычислитель экстремального значения входного кода
В данном случае удобно использовать регистр со входом разрешения записи (ИР27). В регистре сохраняется код экстремума (максимума или минимума), а 8-разрядный компаратор, составленный из двух микросхем СП1, сравнивает содержимое регистра и текущее значение входного кода. Элемент Исключающее ИЛИ выполняет функцию управляемого инвертора, выбирая режим вычисления максимума (единица на управляющем входе) или минимума (нуль на управляющем входе).
Допустим, мы вычисляем максимум. При этом запись в регистр текущего значения входного кода будет производиться только в том случае, когда это текущее значение больше числа, содержащегося в регистре. На выходе ">" компаратора кодов будет тогда сигнал логической единицы, а на входе разрешения записи регистра –WE - сигнал логического нуля. Если же текущее значение входного кода меньше кода, содержащегося в регистре, запись не производится. После окончания входной последовательности кодов (или после окончания одного ее периода при периодической последовательности) в регистре останется максимальное значение входного кода.
Аналогично вычисляется и минимум, только в данном случае в регистр будет записываться не только код, меньший числа в регистре, но и код, равный этому числу. Понятно, что на конечный результат вычисления это никак не повлияет.
